Pyramid Liana

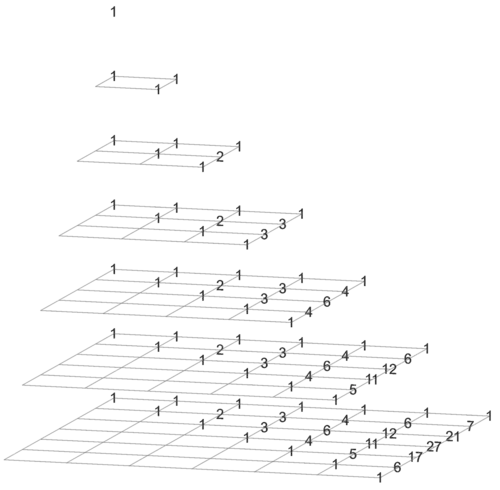
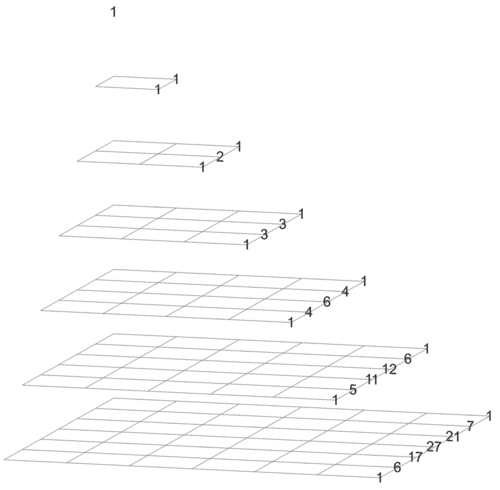
These pyramid pairs are refinements of the triangle pair ^Oak/_[[|Maple]].
In ^Liana/_Ivy the axis valency is added. In ^TwistedLiana/_Lonicera the axis gravity is added.

🌊 Liana and TwistedLiana are refinements of Oak. Their sums along axis depth are Ash and TwistedAsh.

💧 Ivy and Lonicera are refinements of [[|Maple]]. Their sums along axis depth are Aspen and Alder.

Liana and TwistedLiana are essentially the same pyramid: ${\text{Liana}}(a,x,y)={\text{TwistedLiana}}(a,a-x,a-y)$
So ${\text{Liana}}(a,x,y)$ is the cardinality of two sets of $a$ -ary seals: Those with depth $x$ and valency $y$ , and those with depth $a-x$ and gravity $a-y$ .

Pyramids Liana and Ivy


🌊 Liana		💧 Ivy

Only positive coordinates are shown. The column with d = v = 0 is hidden. Liana(a, 0, 0) = 1. Ivy(0, 0, 0) = 1.

equivalents counting houses

(a, d, v) ↦ seals

Liana(a, d, v)
Ivy(a, d, v)

is the number of seals with

arity
adicity

a, depth d and valency v.

🌊 pyramid Liana

overview
Indices in the image go from 1 to 7. Liana is always 1 where depth and valency are 0. But this column is not shown in the images. The sum along valency is triangle *Oak. The sum along depth is triangle Ash. The layer sums (and row sums of these triangles) are sequence Daisy*.

fixed arity (depth × valency matrices)

The row sums are rows of triangle Oak. The column sums are rows of triangle Ash. The total sums are entries of Daisy.

arity 0

v d	0	Σ
0	1	1
1
2
3
4
5
6
7
Σ	1	1

arity 1

v d	0	1	Σ
0	1		1
1		1	1
2
3
4
5
6
7
Σ	1	1	2

arity 2

v d	0	1	2	Σ
0	1			1
1		2	1	3
2			1	1
3
4
5
6
7
Σ	1	2	2	5

arity 3

v d	0	1	2	3	Σ
0	1				1
1		3	3	1	7
2			3	4	7
3				1	1
4
5
6
7
Σ	1	3	6	6	16

arity 4

v d	0	1	2	3	4	Σ
0	1					1
1		4	6	4	1	15
2			6	16	13	35
3				4	11	15
4					1	1
5
6
7
Σ	1	4	12	24	26	67

arity 5

v d	0	1	2	3	4	5	Σ
0	1						1
1		5	10	10	5	1	31
2			10	40	65	40	155
3				10	55	90	155
4					5	26	31
5						1	1
6
7
Σ	1	5	20	60	130	158	374

arity 6

v d	0	1	2	3	4	5	6	Σ
0	1							1
1		6	15	20	15	6	1	63
2			15	80	195	240	121	651
3				20	165	540	670	1395
4					15	156	480	651
5						6	57	63
6							1	1
7
Σ	1	6	30	120	390	948	1330	2825

arity 7

v d	0	1	2	3	4	5	6	7	Σ
0	1								1
1		7	21	35	35	21	7	1	127
2			21	140	455	840	847	364	2667
3				35	385	1890	4690	4811	11811
4					35	546	3360	7870	11811
5						21	399	2247	2667
6							7	120	127
7								1	1
Σ	1	7	42	210	910	3318	9310	15414	29212

fixed depth (arity × valency matrices)

The row sums are columns of triangle Oak.

depth 0

v a	0	Σ
0	1	1
1	1	1
2	1	1
3	1	1
4	1	1
5	1	1
6	1	1
7	1	1

depth 1

v a	1	2	3	4	5	6	7	Σ
0
1	1							1
2	2	1						3
3	3	3	1					7
4	4	6	4	1				15
5	5	10	10	5	1			31
6	6	15	20	15	6	1		63
7	7	21	35	35	21	7	1	127

depth 2

v a	2	3	4	5	6	7	Σ
0
1
2	1						1
3	3	4					7
4	6	16	13				35
5	10	40	65	40			155
6	15	80	195	240	121		651
7	21	140	455	840	847	364	2667

depth 3

v a	3	4	5	6	7	Σ
0
1
2
3	1					1
4	4	11				15
5	10	55	90			155
6	20	165	540	670		1395
7	35	385	1890	4690	4811	11811

depth 4

v a	4	5	6	7	Σ
0
1
2
3
4	1				1
5	5	26			31
6	15	156	480		651
7	35	546	3360	7870	11811

depth 5

v a	5	6	7	Σ
0
1
2
3
4
5	1			1
6	6	57		63
7	21	399	2247	2667

depth 6

v a	6	7	Σ
0
1
2
3
4
5
6	1		1
7	7	120	127

depth 7

v a	7	Σ
0
1
2
3
4
5
6
7	1	1

sum: triangle Ash

v a	0	1	2	3	4	5	6	7	Σ
0	1								1
1	1	1							2
2	1	2	2						5
3	1	3	6	6					16
4	1	4	12	24	26				67
5	1	5	20	60	130	158			374
6	1	6	30	120	390	948	1330		2825
7	1	7	42	210	910	3318	9310	15414	29212

fixed valency (arity × depth matrices)

The row sums are columns of triangle Ash.

valency 0

d a	0	Σ
0	1	1
1	1	1
2	1	1
3	1	1
4	1	1
5	1	1
6	1	1
7	1	1

valency 1

d a	1	Σ
0
1	1	1
2	2	2
3	3	3
4	4	4
5	5	5
6	6	6
7	7	7

valency 2

d a	1	2	Σ
0
1
2	1	1	2
3	3	3	6
4	6	6	12
5	10	10	20
6	15	15	30
7	21	21	42

valency 3

d a	1	2	3	Σ
0
1
2
3	1	4	1	6
4	4	16	4	24
5	10	40	10	60
6	20	80	20	120
7	35	140	35	210

valency 4

d a	1	2	3	4	Σ
0
1
2
3
4	1	13	11	1	26
5	5	65	55	5	130
6	15	195	165	15	390
7	35	455	385	35	910

valency 5

d a	1	2	3	4	5	Σ
0
1
2
3
4
5	1	40	90	26	1	158
6	6	240	540	156	6	948
7	21	840	1890	546	21	3318

valency 6

d a	1	2	3	4	5	6	Σ
0
1
2
3
4
5
6	1	121	670	480	57	1	1330
7	7	847	4690	3360	399	7	9310

valency 7

d a	1	2	3	4	5	6	7	Σ
0
1
2
3
4
5
6
7	1	364	4811	7870	2247	120	1	15414

sum: triangle Oak

d a	0	1	2	3	4	5	6	7	Σ
0	1								1
1	1	1							2
2	1	3	1						5
3	1	7	7	1					16
4	1	15	35	15	1				67
5	1	31	155	155	31	1			374
6	1	63	651	1395	651	63	1		2825
7	1	127	2667	11811	11811	2667	127	1	29212

other sides
valency − depth = 0 Pascal's triangle (with left column not shown)	arity − valency = 0 triangle Birch

💧 pyramid Ivy

overview

Indices in the image go from 1 to 7.
The entry Ivy(0, 0, 0) = 1 is not shown in the images.

The sum along valency is triangle [[|Maple]]. The sum along depth is triangle Aspen.
The layer sums (and row sums of these triangles) are sequence Dahlia.

The pyramid sides in the back (depth = 1) and front (valency − depth = 0) are Pascal's triangle.

fixed adicity (depth × valency matrices)

The row sums are rows of triangle [[|Maple]]. The column sums are rows of triangle Aspen. The total sums are entries of Dahlia.

adicity 0

v d	0	Σ
0	1	1
1
2
3
4
5
6
7
Σ	1	1

adicity 1

v d	1	Σ
0
1	1	1
2
3
4
5
6
7
Σ	1	1

adicity 2

v d	1	2	Σ
0
1	1	1	2
2		1	1
3
4
5
6
7
Σ	1	2	3

adicity 3

v d	1	2	3	Σ
0
1	1	2	1	4
2		2	4	6
3			1	1
4
5
6
7
Σ	1	4	6	11

adicity 4

v d	1	2	3	4	Σ
0
1	1	3	3	1	8
2		3	12	13	28
3			3	11	14
4				1	1
5
6
7
Σ	1	6	18	26	51

adicity 5

v d	1	2	3	4	5	Σ
0
1	1	4	6	4	1	16
2		4	24	52	40	120
3			6	44	90	140
4				4	26	30
5					1	1
6
7
Σ	1	8	36	104	158	307

adicity 6

v d	1	2	3	4	5	6	Σ
0
1	1	5	10	10	5	1	32
2		5	40	130	200	121	496
3			10	110	450	670	1240
4				10	130	480	620
5					5	57	62
6						1	1
7
Σ	1	10	60	260	790	1330	2451

adicity 7

v d	1	2	3	4	5	6	7	Σ
0
1	1	6	15	20	15	6	1	64
2		6	60	260	600	726	364	2016
3			15	220	1350	4020	4811	10416
4				20	390	2880	7870	11160
5					15	342	2247	2604
6						6	120	126
7							1	1
Σ	1	12	90	520	2370	7980	15414	26387

fixed depth (adicity × valency matrices)

The row sums are columns of triangle [[|Maple]].

depth 0

v a	0	Σ
0	1	1
1
2
3
4
5
6
7

depth 1

v a	1	2	3	4	5	6	7	Σ
0
1	1							1
2	1	1						2
3	1	2	1					4
4	1	3	3	1				8
5	1	4	6	4	1			16
6	1	5	10	10	5	1		32
7	1	6	15	20	15	6	1	64

depth 2

v a	2	3	4	5	6	7	Σ
0
1
2	1						1
3	2	4					6
4	3	12	13				28
5	4	24	52	40			120
6	5	40	130	200	121		496
7	6	60	260	600	726	364	2016

depth 3

v a	3	4	5	6	7	Σ
0
1
2
3	1					1
4	3	11				14
5	6	44	90			140
6	10	110	450	670		1240
7	15	220	1350	4020	4811	10416

depth 4

v a	4	5	6	7	Σ
0
1
2
3
4	1				1
5	4	26			30
6	10	130	480		620
7	20	390	2880	7870	11160

depth 5

v a	5	6	7	Σ
0
1
2
3
4
5	1			1
6	5	57		62
7	15	342	2247	2604

depth 6

v a	6	7	Σ
0
1
2
3
4
5
6	1		1
7	6	120	126

depth 7

v a	7	Σ
0
1
2
3
4
5
6
7	1	1

sum: triangle Aspen

v a	0	1	2	3	4	5	6	7	Σ
0	1								1
1		1							1
2		1	2						3
3		1	4	6					11
4		1	6	18	26				51
5		1	8	36	104	158			307
6		1	10	60	260	790	1330		2451
7		1	12	90	520	2370	7980	15414	26387

fixed valency (adicity × depth matrices)

The row sums are columns of triangle Aspen.

valency 0

d a	0	Σ
0	1	1
1
2
3
4
5
6
7

valency 1

d a	1	Σ
0
1	1	1
2	1	1
3	1	1
4	1	1
5	1	1
6	1	1
7	1	1

valency 2

d a	1	2	Σ
0
1
2	1	1	2
3	2	2	4
4	3	3	6
5	4	4	8
6	5	5	10
7	6	6	12

valency 3

d a	1	2	3	Σ
0
1
2
3	1	4	1	6
4	3	12	3	18
5	6	24	6	36
6	10	40	10	60
7	15	60	15	90

valency 4

d a	1	2	3	4	Σ
0
1
2
3
4	1	13	11	1	26
5	4	52	44	4	104
6	10	130	110	10	260
7	20	260	220	20	520

valency 5

d a	1	2	3	4	5	Σ
0
1
2
3
4
5	1	40	90	26	1	158
6	5	200	450	130	5	790
7	15	600	1350	390	15	2370

valency 6

d a	1	2	3	4	5	6	Σ
0
1
2
3
4
5
6	1	121	670	480	57	1	1330
7	6	726	4020	2880	342	6	7980

valency 7

d a	1	2	3	4	5	6	7	Σ
0
1
2
3
4
5
6
7	1	364	4811	7870	2247	120	1	15414

sum: triangle Maple

d a	0	1	2	3	4	5	6	7	Σ
0	1								1
1		1							1
2		2	1						3
3		4	6	1					11
4		8	28	14	1				51
5		16	120	140	30	1			307
6		32	496	1240	620	62	1		2451
7		64	2016	10416	11160	2604	126	1	26387

other sides
valency − depth = 0 Pascal's triangle (trivial column on the left not shown)	adicity − valency = 0 triangle Birch

Pyramids TwistedLiana and Lonicera


🌊 TwistedLiana		💧 Lonicera

equivalents counting houses

(a, d, g) ↦ seals

TwistedLiana(a, d, g)
Lonicera(a, d, g)

is the number of seals with

arity
adicity

a, depth d and gravity g.

🌊 pyramid TwistedLiana

overview
The sum along gravity is triangle *Oak. The sum along depth is TwistedAsh. The layer sums (and row sums of these triangles) are sequence Daisy*.

fixed arity (depth × gravity matrices)

The row sums are rows of Oak. The column sums are rows of TwistedAsh. The total sums are entries of Daisy.

arity 0

g d	0	Σ
0	1	1
1
2
3
4
5
6
7
Σ	1	1

arity 1

g d	0	1	Σ
0	1		1
1		1	1
2
3
4
5
6
7
Σ	1	1	2

arity 2

g d	0	1	2	Σ
0	1			1
1	1	2		3
2			1	1
3
4
5
6
7
Σ	2	2	1	5

arity 3

g d	0	1	2	3	Σ
0	1				1
1	4	3			7
2	1	3	3		7
3				1	1
4
5
6
7
Σ	6	6	3	1	16

arity 4

g d	0	1	2	3	4	Σ
0	1					1
1	11	4				15
2	13	16	6			35
3	1	4	6	4		15
4					1	1
5
6
7
Σ	26	24	12	4	1	67

arity 5

g d	0	1	2	3	4	5	Σ
0	1						1
1	26	5					31
2	90	55	10				155
3	40	65	40	10			155
4	1	5	10	10	5		31
5						1	1
6
7
Σ	158	130	60	20	5	1	374

arity 6

g d	0	1	2	3	4	5	6	Σ
0	1							1
1	57	6						63
2	480	156	15					651
3	670	540	165	20				1395
4	121	240	195	80	15			651
5	1	6	15	20	15	6		63
6							1	1
7
Σ	1330	948	390	120	30	6	1	2825

arity 7

g d	0	1	2	3	4	5	6	7	Σ
0	1								1
1	120	7							127
2	2247	399	21						2667
3	7870	3360	546	35					11811
4	4811	4690	1890	385	35				11811
5	364	847	840	455	140	21			2667
6	1	7	21	35	35	21	7		127
7								1	1
Σ	15414	9310	3318	910	210	42	7	1	29212

fixed depth (arity × gravity matrices)

The row sums are columns of Oak.

depth 0

g a	0	Σ
0	1	1
1	1	1
2	1	1
3	1	1
4	1	1
5	1	1
6	1	1
7	1	1

depth 1

The left column shows the Euler numbers (A000295). Their positive terms are summations of 1, 3, 7, 15, 31...

g a	0	1	Σ
0
1		1	1
2	1	2	3
3	4	3	7
4	11	4	15
5	26	5	31
6	57	6	63
7	120	7	127

depth 2

g a	0	1	2	Σ
0
1
2			1	1
3	1	3	3	7
4	13	16	6	35
5	90	55	10	155
6	480	156	15	651
7	2247	399	21	2667

depth 3

g a	0	1	2	3	Σ
0
1
2
3				1	1
4	1	4	6	4	15
5	40	65	40	10	155
6	670	540	165	20	1395
7	7870	3360	546	35	11811

depth 4

g a	0	1	2	3	4	Σ
0
1
2
3
4					1	1
5	1	5	10	10	5	31
6	121	240	195	80	15	651
7	4811	4690	1890	385	35	11811

depth 5

g a	0	1	2	3	4	5	Σ
0
1
2
3
4
5						1	1
6	1	6	15	20	15	6	63
7	364	847	840	455	140	21	2667

depth 6

g a	0	1	2	3	4	5	6	Σ
0
1
2
3
4
5
6							1	1
7	1	7	21	35	35	21	7	127

depth 7

g a	7	Σ
0
1
2
3
4
5
6
7	1	1

sum: triangle TwistedAsh

g a	0	1	2	3	4	5	6	7	Σ
0	1								1
1	1	1							2
2	2	2	1						5
3	6	6	3	1					16
4	26	24	12	4	1				67
5	158	130	60	20	5	1			374
6	1330	948	390	120	30	6	1		2825
7	15414	9310	3318	910	210	42	7	1	29212

fixed gravity (arity × depth matrices)

The row sums are columns of TwistedAsh.

gravity 0

d a	0	1	2	3	4	5	6	Σ
0	1							1
1	1							1
2	1	1						2
3	1	4	1					6
4	1	11	13	1				26
5	1	26	90	40	1			158
6	1	57	480	670	121	1		1330
7	1	120	2247	7870	4811	364	1	15414

gravity 1

d a	1	2	3	4	5	6	Σ
0
1	1						1
2	2						2
3	3	3					6
4	4	16	4				24
5	5	55	65	5			130
6	6	156	540	240	6		948
7	7	399	3360	4690	847	7	9310

gravity 2

d a	2	3	4	5	6	Σ
0
1
2	1					1
3	3					3
4	6	6				12
5	10	40	10			60
6	15	165	195	15		390
7	21	546	1890	840	21	3318

gravity 3

d a	3	4	5	6	Σ
0
1
2
3	1				1
4	4				4
5	10	10			20
6	20	80	20		120
7	35	385	455	35	910

gravity 4

d a	4	5	6	Σ
0
1
2
3
4	1			1
5	5			5
6	15	15		30
7	35	140	35	210

gravity 5

d a	5	6	Σ
0
1
2
3
4
5	1		1
6	6		6
7	21	21	42

gravity 6

d a	6	Σ
0
1
2
3
4
5
6	1	1
7	7	7

gravity 7

d a	7	Σ
0
1
2
3
4
5
6
7	1	1

sum: triangle Oak

d a	0	1	2	3	4	5	6	7	Σ
0	1								1
1	1	1							2
2	1	3	1						5
3	1	7	7	1					16
4	1	15	35	15	1				67
5	1	31	155	155	31	1			374
6	1	63	651	1395	651	63	1		2825
7	1	127	2667	11811	11811	2667	127	1	29212

other sides
depth − gravity = 0 Pascal's triangle	adicity − depth = 1 almost Pascal's triangle (without right diagonal)

💧 pyramid Lonicera

overview
The sum along gravity is triangle *[[\|Maple]]. The sum along depth is triangle Alder. The layer sums (and row sums of these triangles) are sequence Dahlia*.

fixed adicity (depth × gravity matrices)

The row sums are rows of [[|Maple]]. The column sums are rows of Alder. The total sums are entries of Dahlia.

adicity 0

g d	0	Σ
0	1	1
1
2
3
4
5
6
7
Σ	1	1

adicity 1

g d	1	Σ
0
1	1	1
2
3
4
5
6
7
Σ	1	1

adicity 2

g d	0	1	2	Σ
0
1	1	1		2
2			1	1
3
4
5
6
7
Σ	1	1	1	3

adicity 3

g d	0	1	2	3	Σ
0
1	3	1			4
2	1	3	2		6
3				1	1
4
5
6
7
Σ	4	4	2	1	11

adicity 4

g d	0	1	2	3	4	Σ
0
1	7	1				8
2	12	13	3			28
3	1	4	6	3		14
4					1	1
5
6
7
Σ	20	18	9	3	1	51

adicity 5

g d	0	1	2	3	4	5	Σ
0
1	15	1					16
2	77	39	4				120
3	39	61	34	6			140
4	1	5	10	10	4		30
5						1	1
6
7
Σ	132	106	48	16	4	1	307

adicity 6

g d	0	1	2	3	4	5	6	Σ
0
1	31	1						32
2	390	101	5					496
3	630	475	125	10				1240
4	120	235	185	70	10			620
5	1	6	15	20	15	5		62
6							1	1
7
Σ	1172	818	330	100	25	5	1	2451

adicity 7

g d	0	1	2	3	4	5	6	7	Σ
0
1	63	1							64
2	1767	243	6						2016
3	7200	2820	381	15					10416
4	4690	4450	1695	305	20				11160
5	363	841	825	435	125	15			2604
6	1	7	21	35	35	21	6		126
7								1	1
Σ	14084	8362	2928	790	180	36	6	1	26387

fixed depth (adicity × gravity matrices)

The row sums are columns of [[|Maple]].

depth 0

g a	0	Σ
0	1	1
1
2
3
4
5
6
7

depth 1

g a	0	1	Σ
0
1		1	1
2	1	1	2
3	3	1	4
4	7	1	8
5	15	1	16
6	31	1	32
7	63	1	64

depth 2

g a	0	1	2	Σ
0
1
2			1	1
3	1	3	2	6
4	12	13	3	28
5	77	39	4	120
6	390	101	5	496
7	1767	243	6	2016

depth 3

g a	0	1	2	3	Σ
0
1
2
3				1	1
4	1	4	6	3	14
5	39	61	34	6	140
6	630	475	125	10	1240
7	7200	2820	381	15	10416

depth 4

g a	0	1	2	3	4	Σ
0
1
2
3
4					1	1
5	1	5	10	10	4	30
6	120	235	185	70	10	620
7	4690	4450	1695	305	20	11160

depth 5

g a	0	1	2	3	4	5	Σ
0
1
2
3
4
5						1	1
6	1	6	15	20	15	5	62
7	363	841	825	435	125	15	2604

depth 6

g a	0	1	2	3	4	5	6	Σ
0
1
2
3
4
5
6							1	1
7	1	7	21	35	35	21	6	126

depth 7

g a	7	Σ
0
1
2
3
4
5
6
7	1	1

sum: triangle Alder

g a	0	1	2	3	4	5	6	7	Σ
0	1								1
1		1							1
2	1	1	1						3
3	4	4	2	1					11
4	20	18	9	3	1				51
5	132	106	48	16	4	1			307
6	1172	818	330	100	25	5	1		2451
7	14084	8362	2928	790	180	36	6	1	26387

fixed gravity (adicity × depth matrices)

The row sums are columns of Alder.

gravity 0

d a	0	1	2	3	4	5	6	Σ
0	1							1
1
2		1						1
3		3	1					4
4		7	12	1				20
5		15	77	39	1			132
6		31	390	630	120	1		1172
7		63	1767	7200	4690	363	1	14084

gravity 1

d a	1	2	3	4	5	6	Σ
0
1	1						1
2	1						1
3	1	3					4
4	1	13	4				18
5	1	39	61	5			106
6	1	101	475	235	6		818
7	1	243	2820	4450	841	7	8362

gravity 2

d a	2	3	4	5	6	Σ
0
1
2	1					1
3	2					2
4	3	6				9
5	4	34	10			48
6	5	125	185	15		330
7	6	381	1695	825	21	2928

gravity 3

d a	3	4	5	6	Σ
0
1
2
3	1				1
4	3				3
5	6	10			16
6	10	70	20		100
7	15	305	435	35	790

gravity 4

d a	4	5	6	Σ
0
1
2
3
4	1			1
5	4			4
6	10	15		25
7	20	125	35	180

gravity 5

d a	5	6	Σ
0
1
2
3
4
5	1		1
6	5		5
7	15	21	36

gravity 6

d a	6	Σ
0
1
2
3
4
5
6	1	1
7	6	6

gravity 7

d a	7	Σ
0
1
2
3
4
5
6
7	1	1

sum: triangle Maple

d a	0	1	2	3	4	5	6	7	Σ
0	1								1
1		1							1
2		2	1						3
3		4	6	1					11
4		8	28	14	1				51
5		16	120	140	30	1			307
6		32	496	1240	620	62	1		2451
7		64	2016	10416	11160	2604	126	1	26387

other sides
depth − gravity = 0 Pascal's triangle (with trivial column on the left)	adicity − depth = 1 almost Pascal's triangle (without right diagonal, next reduced by 1)